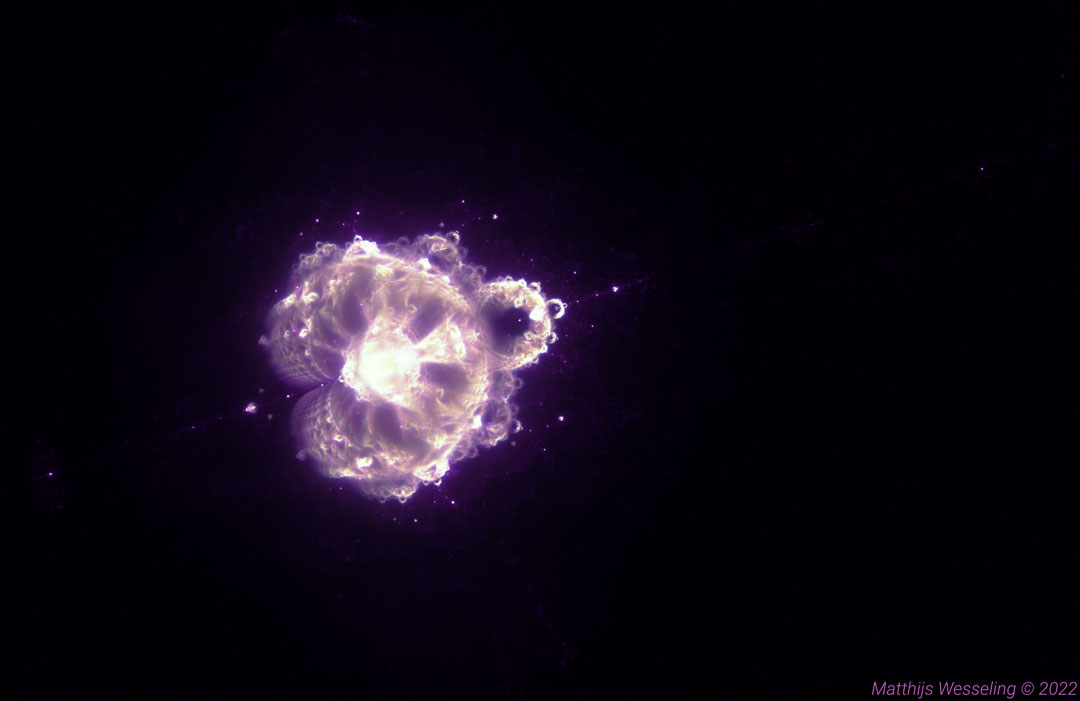
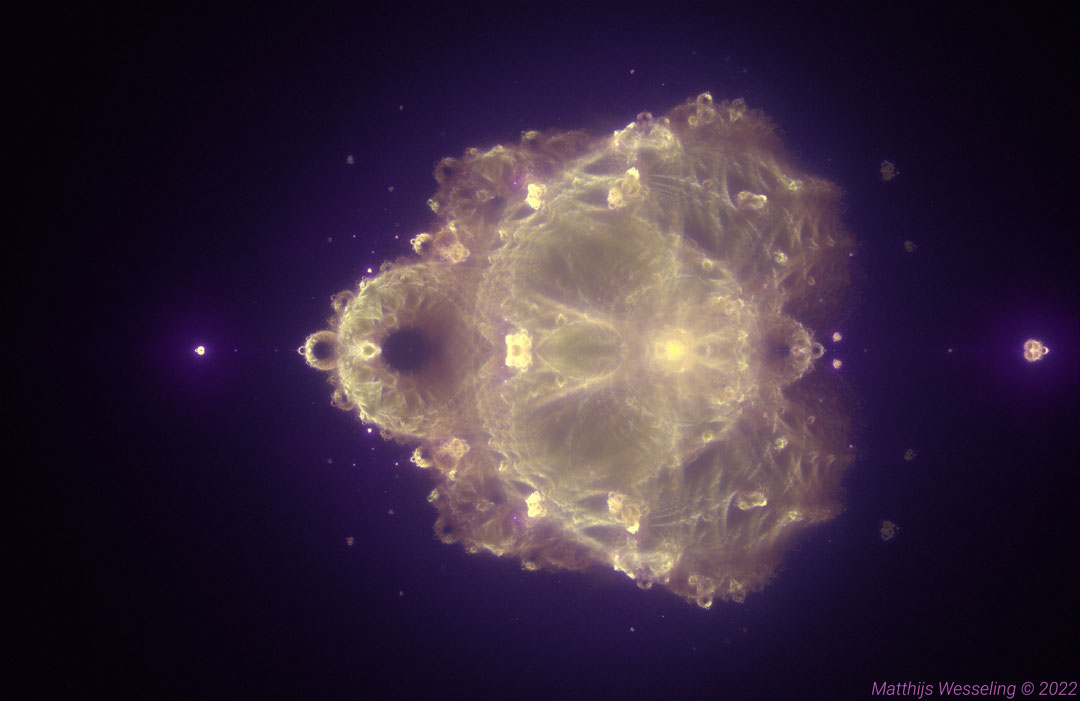
The Buddhabrot Fractal

The classic Mandelbrot fractal is rendered using the quadratic equation:$$z_{n+1} = z_n^2 + c$$Here, $c$ is a constant determined by the location of the pixel. By iterating this equation, a sequence of coordinates in the complex plane is generated. During the iteration, many points will eventually grow exponentially in magnitude and escape to infinity. The escape time is determined by how long it takes for the absolute value of $z$ to reach a certain threshold, indicating that it has escaped to infinity. Points that do not escape are considered to be inside the Mandelbrot set and are typically rendered as black. By selecting an appropriate color scheme, captivating images can be created.

This approach only uses a small part of the available information, as all details about the path except for the length are discarded. The Buddhabrot fractal takes a different approach to rendering the set, by drawing the entire path of all the points that escape. This greatly increases the computational cost of rendering the fractal. In the classical rendering, the contribution of long paths only becomes significant when deep zooms are generated. In the case of the Buddhabrot however, these paths contribute even when fully zoomed out. Resolving this issue requires proper sampling of the constant $c$.

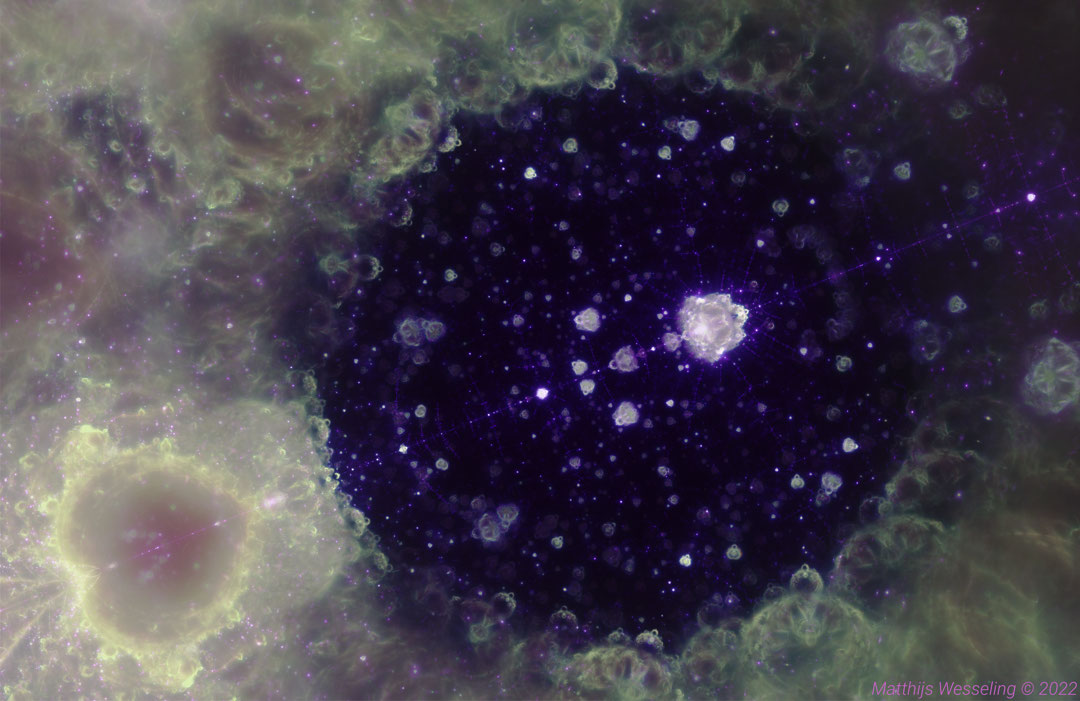
The sampling problem becomes especially apparent when trying to zoom in on the Buddhabrot. The initial values of $c$ that contribute to the image are generally spread out across the complex plane, and finding these contributing areas can be very difficult.

One method to speed up rendering the fractal is the metropolis hastings algorithm. This famous algorithm was first used in the field of statistical physics and allows for sampling of complicated probability distributions. In the context of the buddhabrot fractal, it helps selecting points that contribute to the image. The basic idea of the algorithm is to take an initial point $c$ and perturb it. New candidate coordinates are accepted based on a scoring function. By choosing the correct scoring function, rendering the Buddhabrot fractal can be sped up significantly.